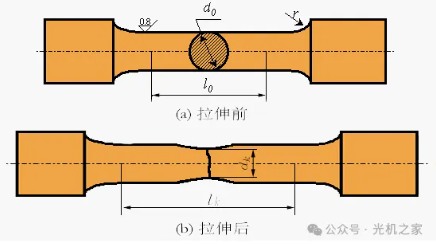
Examen tensile roboris praecipue adhibetur ad facultatem materiarum metallicarum resistendi damno durante processu extensionis determinandam, et est unus ex indicibus magni momenti ad proprietates mechanicas materiarum aestimandas.
1. Experimentum tensile
Examen tensile in principiis fundamentalibus mechanicae materialium nititur. Applicando onus tensile specimini materiali sub certis condicionibus, deformatio tensile efficitur donec specimen frangitur. Per experimentum, deformatio speciminis experimentalis sub variis oneribus et onus maximum cum specimen frangitur notantur, ut firmitas elastica, firmitas tensile, et alii indices effectuum materiae calculentur.
Tensio σ = F/A
σ est robur tensile (MPa)
F est onus tensile (N)
A est area sectionis transversalis speciminis
2. Curva tensa
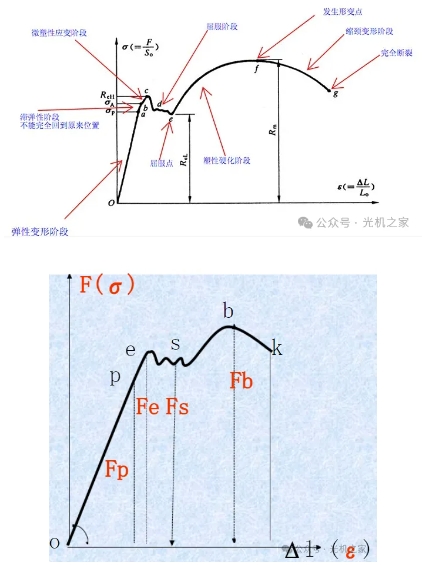
Analysis plurium stadiorum processus extensionis:
a. In stadio OP cum onere parvo, elongatio est in relatione lineari cum onere, et Fp est onus maximum ad lineam rectam conservandam.
b. Postquam onus Fp excedit, curva tensile relationem non linearem habere incipit. Exemplum in stadium deformationis initialem intrat, et onus removetur, et exemplum ad statum pristinum redire et elasticiter deformari potest.
c. Postquam onus Fe excedit, onus removetur, pars deformationis restituitur, et pars deformationis residuae retinetur, quae deformatio plastica appellatur. Fe limes elasticus appellatur.
d. Cum onus ulterius crescit, curva tensile serram formam ostendit. Cum onus neque crescit neque decrescit, phaenomenon elongationis continuae exemplaris experimentalis cessivitas appellatur. Post cessivitatem, exemplar deformationem plasticam manifestam subire incipit.
e. Post cessionem, exemplum ostendit augmentum resistentiae deformationis, duritiem laboris et corroborationem deformationis. Cum onus Fb attingit, eadem pars exempli acriter contrahitur. Fb est limes roboris.
f. Phaenomenon contractionis ad decrementum capacitatis sustinendi exemplaris ducit. Cum onus Fk attingit, exemplar frangitur. Hoc onus fracturae appellatur.
Vis Cedendi
Limitatio elasticitatis est maxima vis tensionis quam materia metallica ab initio deformationis plasticae usque ad fracturam perfectam sustinere potest, cum vi externa subiecta est. Hic valor punctum criticum indicat ubi materia a stadio deformationis elasticae ad stadium deformationis plasticae transit.
Classificatio
Limitatio cessionis superior: ad maximam tensionem exemplaris refertur antequam vis primum decrescit cum cessionis fit.
Limitatio cessionis inferior: ad minimam tensionem in stadio cessionis refertur cum effectus transiens initialis neglegitur. Cum valor limitis cessionis inferioris relative stabilis sit, plerumque ut index resistentiae materiae adhibetur, quod punctum cessionis vel limitatio cessionis appellatur.
Formula calculi
Pro superiore limite cessionis: R = F / Sₒ, ubi F est vis maxima antequam vis primum in stadio cessionis decrescit, et Sₒ est area sectionis transversalis originalis exempli.
Pro minore limite elasticitatis: R = F / Sₒ, ubi F est vis minima F neglecto effectu initiali transeunte, et Sₒ est area sectionis transversalis originalis exempli.
Unitas
Unitas limitis elasticitatis plerumque est MPa (megapascal) vel N/mm² (Newton per millimetrum quadratum).
Exemplum
Exempli gratia, chalybs carbonis humilis sume, cuius limes flexionis plerumque 207MPa est. Cum vi externa maiori quam hoc limine subiectus est, chalybs carbonis humilis deformationem permanentem producet nec restitui potest; cum vi externa minore quam hoc limine subiectus est, chalybs carbonis humilis ad statum pristinum redire potest.
Limitatio elasticitatis est unus e magnis indicibus ad proprietates mechanicas materiarum metallicarum aestimandas. Repraesentat facultatem materiarum deformationi plasticae resistendi cum viribus externis subiectae sunt.
Robur tensile
Robur tensile est facultas materiae resistendi damnum sub onere tensile, quae specifice exprimitur ut valor maximus tensionis quem materia sustinere potest durante processu tensile. Cum tensio tensile in materia excedit suam vim tensilem, materia deformationem plasticam seu fracturam subibit.
Formula calculi
Formula computandi pro robore tensile (σt) est:
σt = F / A
Ubi F est maxima vis tensile (Newton, N) quam specimen sustinere potest ante fractionem, et A est area sectionis transversalis originalis speciminis (millimetrum quadratum, mm²).
Unitas
Unitas roboris tensilis plerumque est MPa (megapascal) vel N/mm² (Newton per millimetrum quadratum). 1 MPa aequale est 1,000,000 Newtonorum per metrum quadratum, quod etiam aequale est 1 N/mm².
Factores influentes
Robur tensile a multis factoribus afficitur, inter quos sunt compositio chemica, microstructura, processus tractationis caloris, modus processus, et cetera. Materiae diversae diversas vires tensiles habent, ergo in applicationibus practicis, necesse est materias idoneas eligere secundum proprietates mechanicas materiarum.
Applicatio practica
Robur tensile est parametrus magni momenti in campo scientiae et artis ingeniariae materialium, et saepe adhibetur ad proprietates mechanicas materiarum aestimandas. Quod ad designationem structurae, delectum materiae, aestimationem salutis, et cetera attinet, robur tensile est factor qui considerandus est. Exempli gratia, in arte ingeniaria constructionis, robur tensile ferri est factor magni momenti ad determinandum utrum onera sustinere possit; in campo aëronautico, robur tensile materiarum levium et magnae firmitatis est clavis ad salutem aeroplanorum confirmandam.
Robur lassitudinis:
Fatigatio metallorum ad processum refertur quo materiae et componentes paulatim damnum cumulativum locale permanens in uno vel pluribus locis sub tensione cyclica vel deformatione cyclica producunt, et fissurae vel fracturae subitae completae post certum numerum cyclorum fiunt.
Proprietates
Subitanea temporis ratio: Ruptura lassitudinis metallicae saepe subito brevi tempore sine signis manifestis accidit.
Situs in situ: Defatigatio plerumque in locis localibus ubi tensio concentratur accidit.
Sensibilitas ad ambitum et vitia: Fatigatio metalli valde sensibilis est ad ambitum et minima vitia intra materiam, quae processum fatigationis accelerare possunt.
Factores influentes
Amplitudo tensionis: Magnitudo tensionis directe afficit vitam lassitudinis metalli.
Magnitudo tensionis mediae: Quo maior tensio media, eo brevior vita lassitudinis metalli.
Numerus cyclorum: Quo saepius metallum sub tensione vel tensione cyclica est, eo gravior accumulatio damni lassitudinis.
Mensurae praecavendae
Delectum materiae optimiza: Materias cum limitibus lassitudinis altioribus elige.
Concentrationem tensionis minuere: Concentrationem tensionis per designationem structuralem vel methodos processus reducere, ut transitiones angulorum rotundatorum utendo, dimensiones sectionis transversalis augendo, etc.
Curatio superficiei: Politura, aspersio, etc. in superficie metallica ad vitia superficialia minuenda et roborandam resistentiam lassitudinis.
Inspectio et conservatio: Partes metallicas regulariter inspice ut vitia, ut rimas, celeriter detegantur et reparentur; partes defatigationi obnoxias conserva, ut partes detritas substituas et nexus debiles confirmes.
Fatigatio metallorum modus communis fractionis metallorum est, qui repentinitate, loco, et sensibilitate ad ambitum insignitur. Amplitudo tensionis, magnitudo tensionis media, et numerus cyclorum sunt factores principales qui fatigationem metallorum afficiunt.
Curva SN: vitam lassitudinis materiarum sub variis gradibus tensionis describit, ubi S tensionem et N numerum cyclorum tensionis repraesentat.
Formula coefficientis roboris lassitudinis:
(Kf = Ka ∫Kb ∫Kc ∫Kd ∫Ke)
Ubi (Ka) est factor oneris, (Kb) est factor magnitudinis, (Kc) est factor temperaturae, (Kd) est factor qualitatis superficiei, et (Ke) est factor fidutiae.
Expressio mathematica curvae SN:
(\sigma^m N = C)
Ubi (σ) est tensio, N est numerus cyclorum tensionis, et m et C sunt constantes materiales.
Gradus calculi
Constantes materiales determina:
Valores m et C per experimenta vel per consultationem litterarum pertinentium determina.
Determina factorem concentrationis tensionis: Considera formam et magnitudinem actualem partis, necnon concentrationem tensionis a angulis, foraminibus clavium, etc. causatam, ad determinandum factorem concentrationis tensionis K. Calcula robur lassitudinis: Secundum curvam SN et factorem concentrationis tensionis, una cum vita designata et gradu tensionis operativae partis, calcula robur lassitudinis.
2. Plasticitas:
Plasticitas ad proprietatem materiae refertur, quae, vi externae subiecta, deformationem permanentem sine fractione producit, cum vis externa limitem elasticitatis excedit. Haec deformatio irreversibilis est, et materia ad formam pristinam non redibit etiam si vis externa sublata sit.
Index plasticitatis et formula eius computandi
Elongatio (δ)
Definitio: Elongatio est percentatio deformationis totalis sectionis mensurae postquam specimen ad longitudinem mensurae originalem fractum est per tensile.
Formula: δ = (L1 - L0) / L0 100%
Ubi L0 est longitudo mensurae originalis speciminis;
L1 est longitudo mensurae postquam specimen fractum est.
Reductio segmentalis (Ψ)
Definitio: Reductio segmentalis est percentatio maximae reductionis in area sectionis transversalis ad punctum strinctionis postquam specimen ad aream sectionis transversalis originalem fractum est.
Formula: = (F0 - F1) / F0 100%
Ubi F0 est area sectionis transversalis originalis speciminis;
F1 est area sectionis transversalis ad punctum strinctionis postquam specimen fractum est.
3. Duritia
Durities metallorum est index proprietatum mechanicarum ad duritiem materiarum metallicarum metiendam. Indicat facultatem deformationi resistendi in volumine locali superficiei metallicae.
Classificatio et repraesentatio duritiae metalli
Durities metallorum variis modis classificationis et repraesentationis secundum varias probationum rationes habet. Praecipue haec comprehendunt:
Durities Brinell (HB):
Ambitus applicationis: Generaliter adhibetur cum materia mollior est, ut in metallis non ferreis, chalybs ante curationem caloris vel post recoctionem.
Principium probationis: Cum certa magnitudine oneris probationis, pila chalybis indurati vel pila carburi diametri certi in superficiem metalli probandi premitur, et onus post tempus definitum exoneratur, et diameter indentationis in superficie probanda metitur.
Formula calculi: Durities Brinell est quotiens obtentus dividendo onus per aream superficiei sphaericae indentationis.
Duritia Rockwelliana (HR):
Ambitus applicationis: Generaliter adhibetur pro materiis cum maiori duritia, ut puta duritia post curationem caloris.
Principium probationis: Simile duritiae Brinell, sed utens diversis specillis (adamantis) et diversis methodis computationis.
Genera: Pro applicatione, sunt HRC (pro materiis altae duritiae), HRA, HRB et alia genera.
Durities Vickers (HV):
Ambitus applicationis: Idoneus ad analysin microscopicam.
Principium probationis: Superficiem materiae preme cum onere minore quam 120kg et indentatore conico quadrato adamantino cum angulo verticis 136°, et aream superficiei foveae indentationis materiae divide per valorem oneris ut valorem duritiae Vickers obtineas.
Duritia Leebiana (HL):
Proprietates: Duritiem probans portabilis, facile metiendus.
Principium probationis: Utere saltu a capite sphaerico impactus generato post impactum in superficiem duritiei, et duritiam computa per rationem celeritatis resilitionis punch ad 1mm a superficie exempli ad celeritatem impactus.
Tempus publicationis: XXV Septembris, MMXXIV